pushing the limits

Performing higher order FFTs on ultra low power MSP 430 micro controllers

Fourier Transforms: A quick introduction

Since their discovery in the mid 18th century, frequency analysis techniques have come a long way today. From their simple beginnings in astronomy and heat transfer studies, these techniques can now be found in almost every engineering field as well as in areas like statistics and finance which depend heavily on analyzing trends. The widespread use of frequency analysis can be attributed primarily to the development of the Fast Fourier Transform (FFT). Generating a frequency domain representation of a signal is essentially solving a large system of equations with conventional techniques from linear algebra. The FFT however acknowledges repeating patterns that are generated during this process and leverages them to speed up the process greatly.

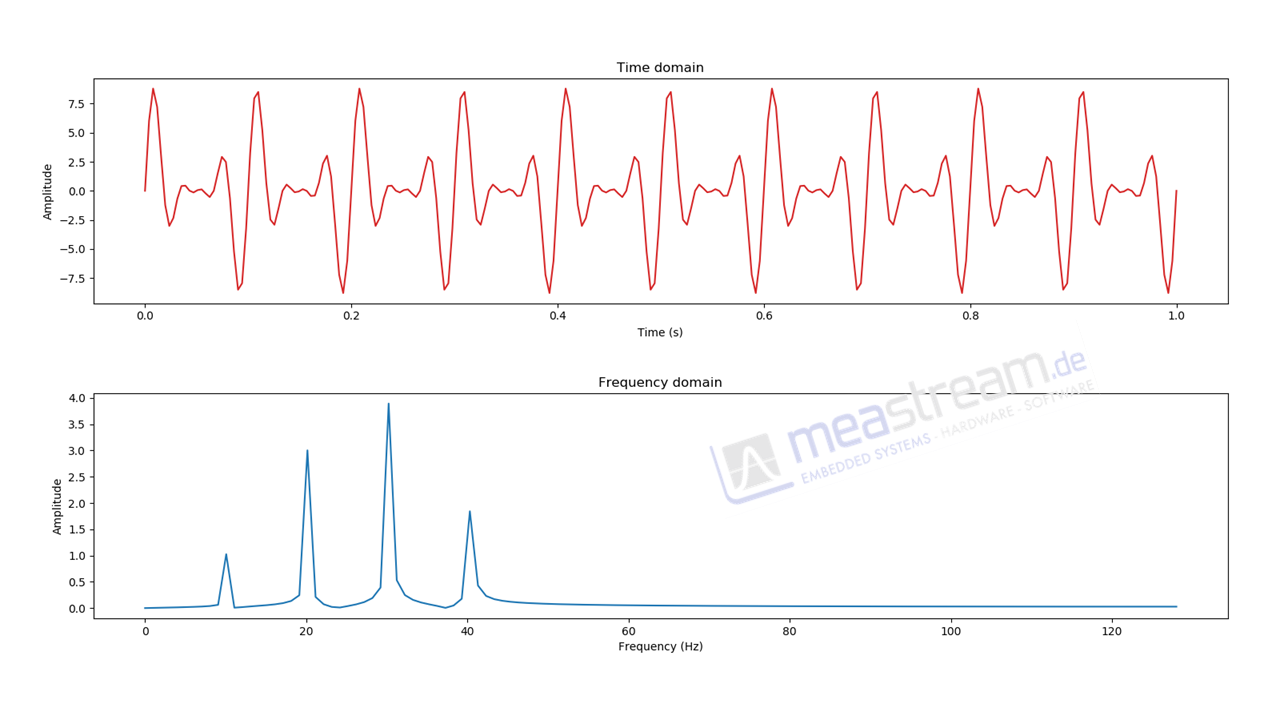
The image below shows a time domain signal sampled over the duration of one second. Although a slight trend can be recognized in the upper frame, the true content of the signal is revealed in its frequency domain representation in the lower frame. One can see that the signal consists of four individual components with varying amplitudes and frequencies.

FFTs and low power micro controllers

The need for implementing FFT calculations on electronic hardware was recognized very early resulting in the introduction of specialized Digital Signal Processors (DSP). With the passage of time, many micro controller manufacturers have started integrating the core elements of a DSP in regular micro controllers. This has given a boost to the application of low power micro controllers in diverse engineering fields. Being able to perform a complex calculation like the FFT locally on the micro controller has many benefits. Firstly, any analysis required can be performed in real time, cutting down on the delay required to transfer packets of data to an external system. This is especially beneficial for systems that control processes instead of just monitoring them. Secondly, the amount of data transferred by the system reduces greatly leading to a simplified design in general. Most implementations of FFTs on micro controllers though rely on simple addition and multiplication calculations meaning that the controller is actively focused on the calculation while consuming large amounts of energy by running at a high frequency.

FFTs and the MSP 430

The MSP 430 family of micro controllers from Texas Instruments addresses the above issues by including a Low Energy Accelerator (LEA) unit in some micro controllers. The LEA supports in-situ calculations with vectors of numbers making it ideal for a diverse range of mathematical calculations. Of primary interest to higher order FFTs are the complex multiplication and complex addition functions. The LEA also supports FFT calculations with vectors of up to 1024 (1K) points. While sufficient for simple analysis, a lot of applications demand the ability to perform larger FFTs up to 8K or even 16K points. The largest FFT that can be performed depends on the amount of memory available on the chip. The current available memory sizes make it possible to perform 16K FFTs in some cases on the micro controller.

The leap from 1K to 16K

FFT calculations are based on a divide and conquer method where a large problem is essentially seen as a collection of similar, smaller problems. The very first step involves calculating so called 2-point FFTs. The results of these calculations can then be combined to generate 4-Point FFTs and so on till any higher power of 2. Since the local LEA unit already performs 1024-Point FFTs (210) a large part of the calculation is done already. Our algorithm now steps in to combine these “smaller” FFTs to generate larger FFTs. For this, we first rearrange the data vector and then perform the LEA FFTs to align our results for the next step. Then we use the LEA vector operations (complex addition and complex multiplication) to generate higher order FFTs.

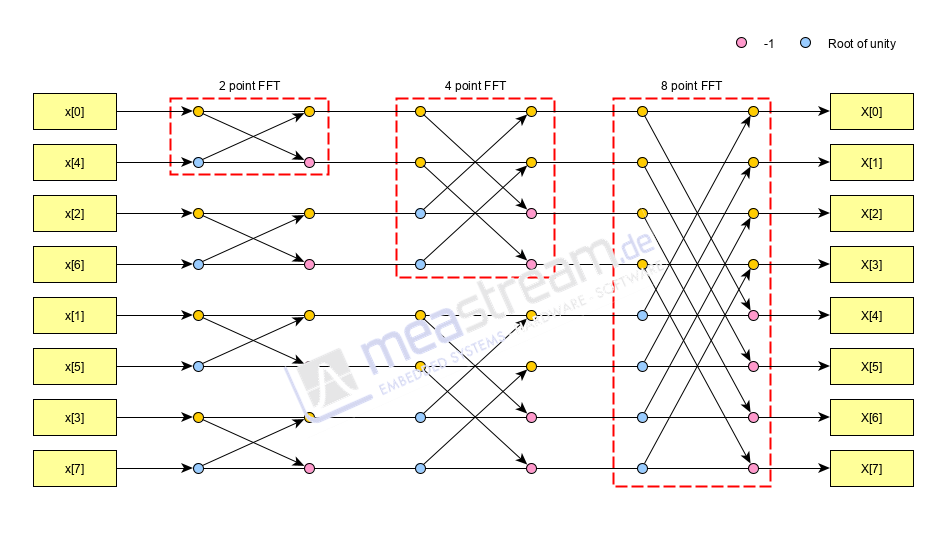
The image above shows how an 8-point FFT is generated by combining multiple smaller FFTs. Similarly, one can imagine how eight 1K FFTs can be combined to generate an 8K FFT. The only change will be that instead of single points we will be dealing with 1024 point vectors.

Applications

The ability to locally perform complex calculations like an 8K point FFT opens up many possibilities to move dedicated functionality to smaller micro controllers. One sample application could be for a simple vibration analysis in an automobile where just the results of the vibration analysis can be transferred to another ECU via the LIN bus. This would reduce system costs as such an application would traditionally include a more powerful micro controller wired over the CAN interface. Another application would be the use of preprocessed data for condition monitoring and predictive maintenance in manufacturing.